Hilbert Matrices
Prove that the matrix given by
\[
\begin{bmatrix}
1 & \frac 12 & \dots & \frac 1n\\
\frac 12 & \frac 13 & \dots & \frac 1{n+1}\\
\vdots & \vdots & \ddots & \vdots\\
\frac 1n & \frac 1{n+1} & \dots & \frac 1{2n-1}\\
\end{bmatrix}
\]
is non-singular.
Solution. Observe that if we denote the matrix above with \(H = [H_{ij}]\), then we have
\[
H_{ij} = \int_{0}^{1} x^{i+j-2}.
\]
Now let \( \vec{x} = (x_1, x_2, \dots, x_n)^\intercal \neq \vec 0\) be an arbitrary column vector. Some straightforward calculations give:
\[
\begin{align}
\vec{x}^\intercal H \vec{x}
&= \sum_{i, j=1}^{n}\left(x_i x_j\int_{0}^{1} x^{i+j-2}\right)dx\\
&= \int_{0}^{1}\left(\sum_{i=1}^{n} x_ix^{i-1}\right)^2 dx > 0.
\end{align}
\]
Therefore, the only solution to the equation \(H\vec x = \vec 0\) is the trivial solution and the conclusion follows. ▢Simple but Fun
Suppose \(n\) is an odd number and \(a_1, a_2, \dots, a_n\) is a permutation of \(1, 2, \dots, n\). Prove that the product
\[
(a_1-1)\cdot(a_2-2)\dots (a_n-n)
\]
is always an even number.
Solution. One only need to observe that
\[
(a_1-1) + (a_2-2) + \dots + (a_n-n) = 0.
\]
As the sum of an odd number of integers results in zero, at least one of them should be even. ▢Trigonometry Without a Word
Prove the following two equalities
\[
\arctan(\frac 12) + \arctan(\frac 13) = \frac \pi 4\\
\arctan(1) + \arctan(2) + \arctan(3) = \pi.
\]
Solution. 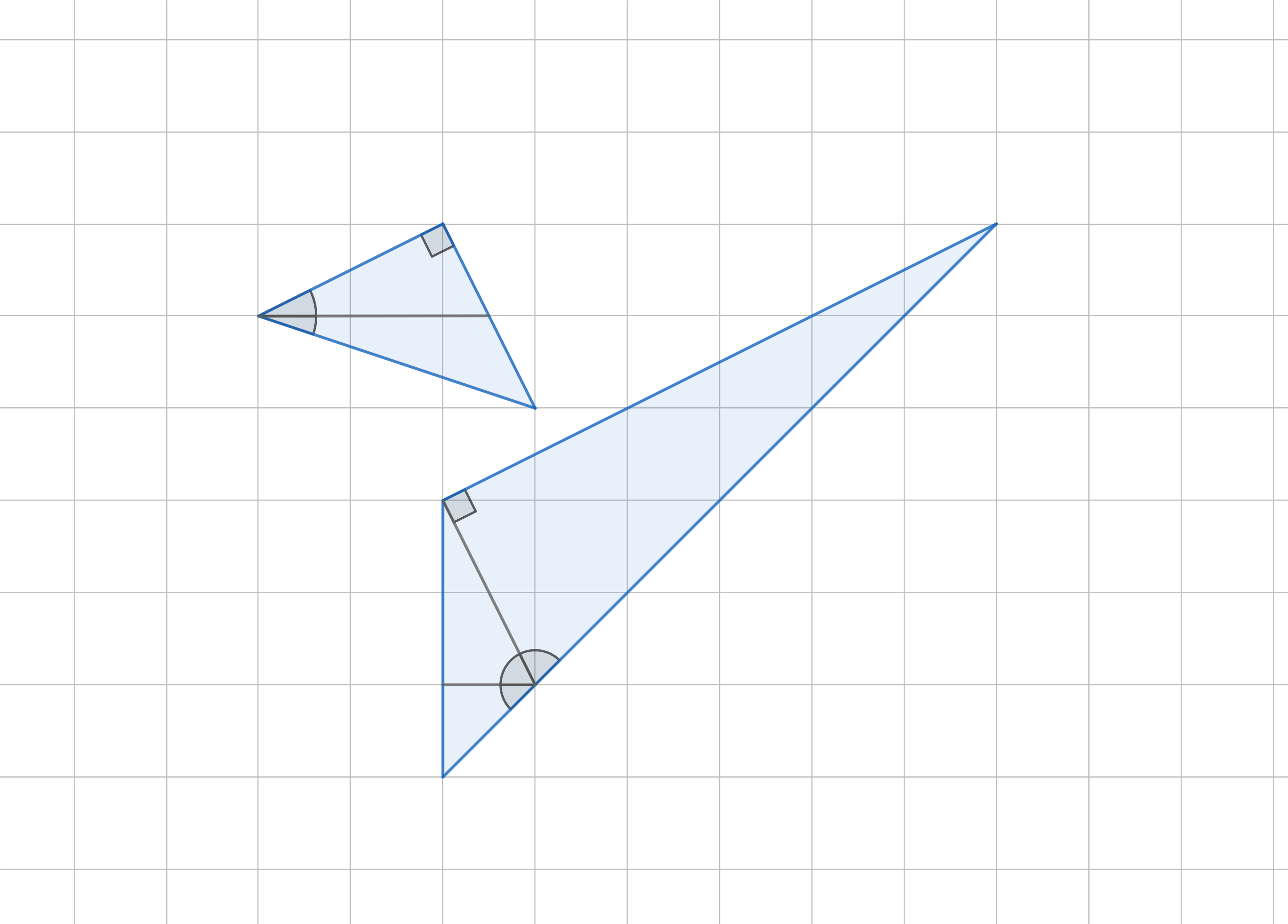
A Without-a-Word Proof

Conservative Polynomials
Suppose that \(P\) is a polynomial that takes both positive and negative values. Prove that the function \(|P|\) is not a polynomial anymore.
Solution. Suppose to the contrary that \(|P|\) is a polynomial and without loss of generality also suppose that \(P\) takes positive values infinitely many times. Therefore the polynomial equality \(|P(x)| - P(x) = 0\) has infinitely many solutions. Hence the fundamental theorem of algebra gives \(|P(x)| = P(x)\) which contradicts the fact that \(P\) takes both positive and negative values. ▢
Stirling's Approximation but Weaker
Show that
\[
\lim_{n\to \infty} \frac{e^nn!}{n^n} = \infty.
\]
Solution. Fix \(k\in \mathbb N\). According to the power series representation of the exponential function we should have:
\[
\begin{align*}
e^n
&= 1 + n + \frac{n^2}{2!} + \cdots + \frac{n^n}{n!} + \frac{n^{n+1}}{(n+1)!} + \cdots\\
&\gt \frac{n^n}{n!}\left(1 + \frac {n}{n+1} + \frac {n^2}{(n+1)(n+2)}+ \cdots\right)\\
&\gt \frac{n^n}{n!}\left(1 + \frac {n}{n+1} + \cdots + \frac {n^k}{(n+1)\cdots(n+k)}\right).\tag{1}\label{eq:1}
\end{align*}
\]
Therefore, \ref{eq:1} gives
\[
\liminf_{n\to \infty} \frac{e^nn!}{n^n} \gt k
\]
and the conclusion follows from the fact that \(k\) was an arbitrary number. ▢